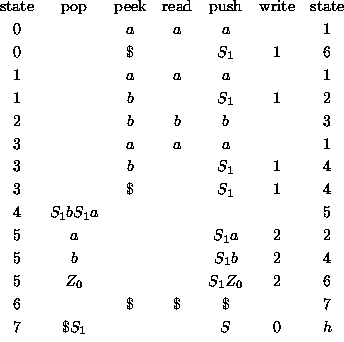Consider the unambiguous context-free grammar G, whose productions are given as follows:
0. 
1. 
2. 
Let L=L(G). The problem is to design a shift-reduce parser for G. Note that G is unambiguous.
Although the textbook does not mention it, we would like the parser to
output the derivation of any input string in L. In this case, the
derivation will be the so-called ``reverse rightmost'' derivation of the
string. For example, if the input string is 
, then the output
of the parser should be 11211220.
Here is the table of the transitions that we want our parser to make.
Note that we do not concern ourselves with states at this time, and we
allow the popping of any number of symbols in one step. Nor do we concern
ourselves with lookahead, because we have not yet figured out how to use
lookahead as a guide. We call this machine, which always knows what to
do without having any memory or lookahead, 
.
We now look at the sequence of configurations that occurs when
parses .
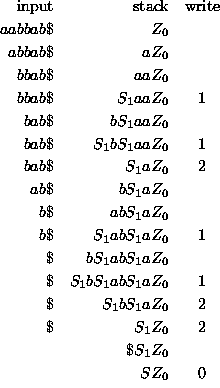
We now design a deterministic lookahead parser 
that emulates the
action of . can look ahead (``peek'') without reading.
has 8 states. We write just numbers for the states, for example,
4 symbolizes state 
. It helps to write an explanation for each
state in words.
If the entry in the ``peek'' column is empty, that means that
does not need to look ahead to perform that transition. We allow
to pop any number (zero or more) of symbols.
is deterministic, but is not
yet a DPDA according to the formal rules, because those rules require
that exactly one symbol be popped at every step.
